Just for the fun of it, and to see if it could be done, I started playing with fractals in R. I was really surpised to see R's suitability for handling these mathematical objects. In fact, the easiness of integrating C code with R and R's graphics capabilities makes R superbly fitted for this purpose (perhaps even more than some 'professional' fractal generators).

This page contains some beautiful images created with R and the code needed to generate them. Some functions are linked to C code, but don't get scared! R's documentation contains plenty of material on how to compile and use shared objects.

The logistic equation

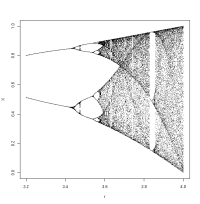
There is a special case of the logistic equation of population growth that shows some surprisingly complex behavior. This deceptively simple function is

Xi+1 = r * Xi * (1 - Xi)

where Xi is the relative population size at time i, Xi+1 is the size at the next generation and  r is the  growth rate. In this model X varies between 0 and 1. The interesting point here is that for r values below ~3.5 the population will reach a stationary size after many generations or will oscillate between a set of fixed values; however, when r is higher than ~3.5 the system becomes chaotic and the population size will oscillate in a seemingly random manner. The picture above shows what happens to X after 50 or more generations under different r values. The code to generate that graph is here: logistic.R.

The Mandelbrot set

Perhaps the most famous fractal set. It arises from a very simple mathematical relationship

Zi+1 = Zi * Zi + C

where Z and C are complex numbers (e.g. a + bi ). The initial value of Z, Z0 is equal to 0, and the value of C is chosen arbitrarily. Then succesive iterations of the above equation are calculated, and the evolution of Z is assesed. It can be mathematically proved that if after certain number of iterations the modulus of Z is greater than 2, then the value of Z will head off to infinity. The Mandelbrot set is then defined as the set of points C in the complex plane for which the iteration procedure is bound (i.e. doesn't head off to infinity!). Bellow is a small galery of pictures depicting different regions of the Mandelbrot set; points belonging to the set are shown in black, and the rest are coloured according to the number of iterations needed for |Z| > 2.

The files needed to generate images like the ones above are here: mandelbrot.zip

---

Any question or comments please e-mail me at_mariodosreis@yahoo.com
I am willing to accept any kind of fractal stuff done with R!
Update December 2016: The Mandelbrot set is now in my R fractal package: github.com/mariodosreis/fractal